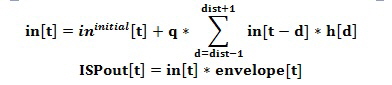|
|
 |
||||
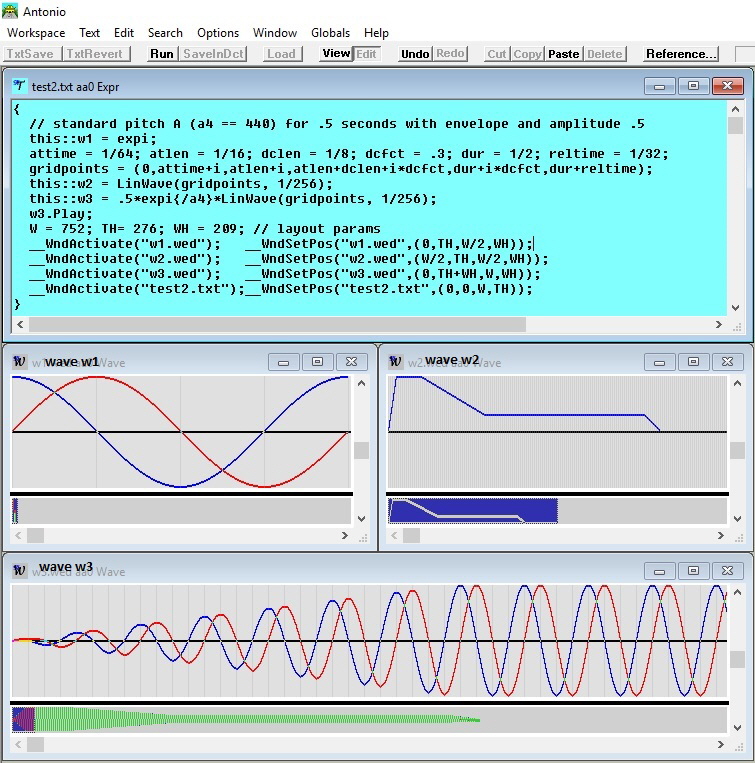
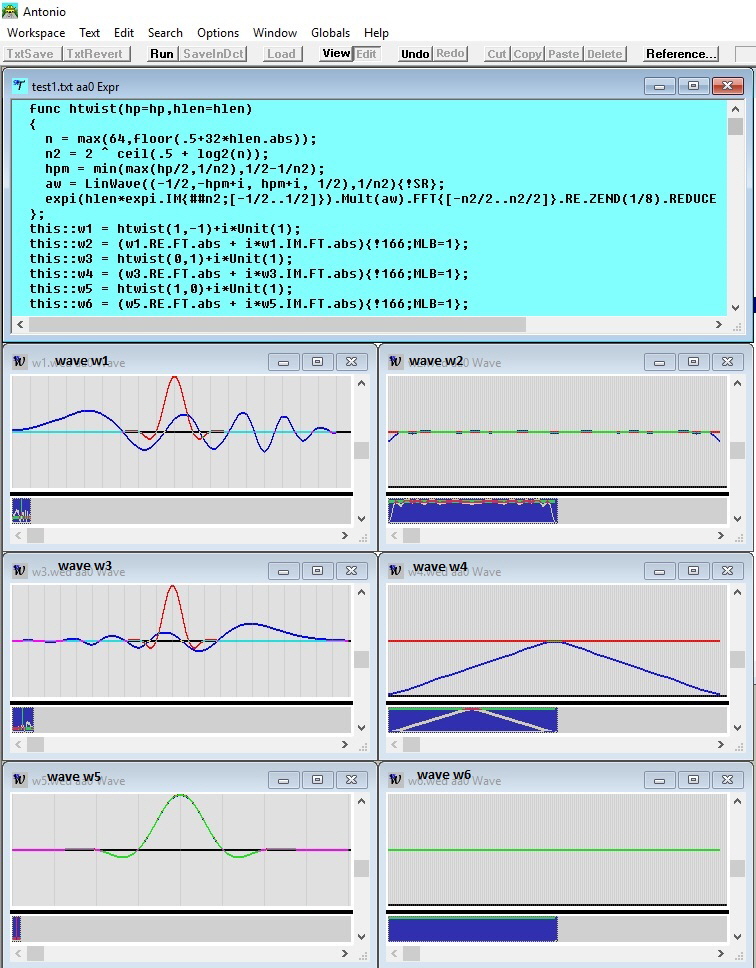
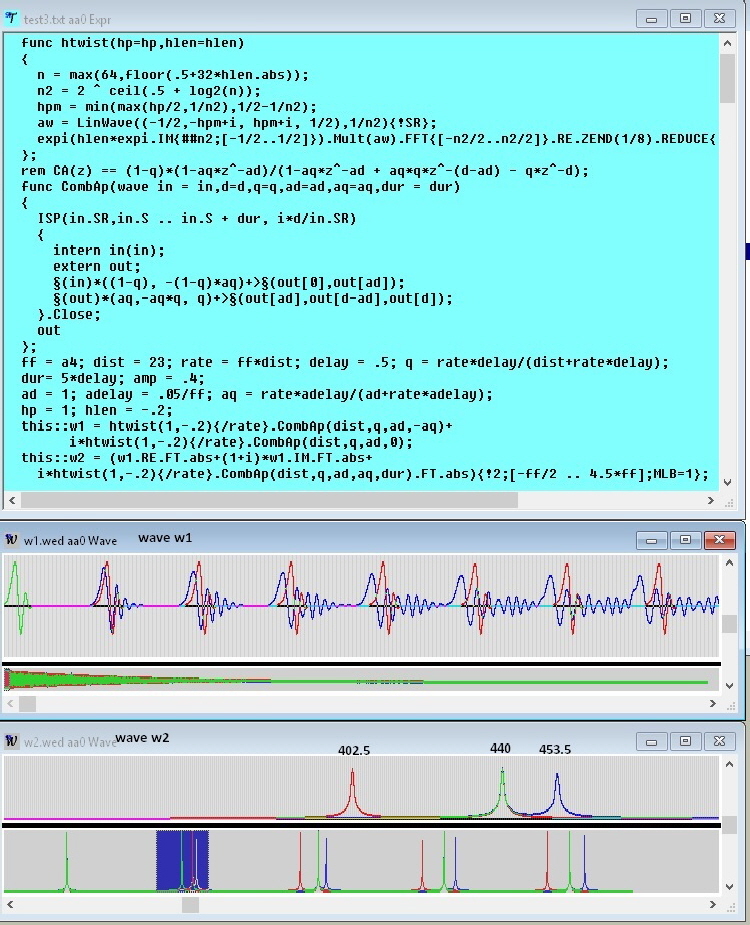
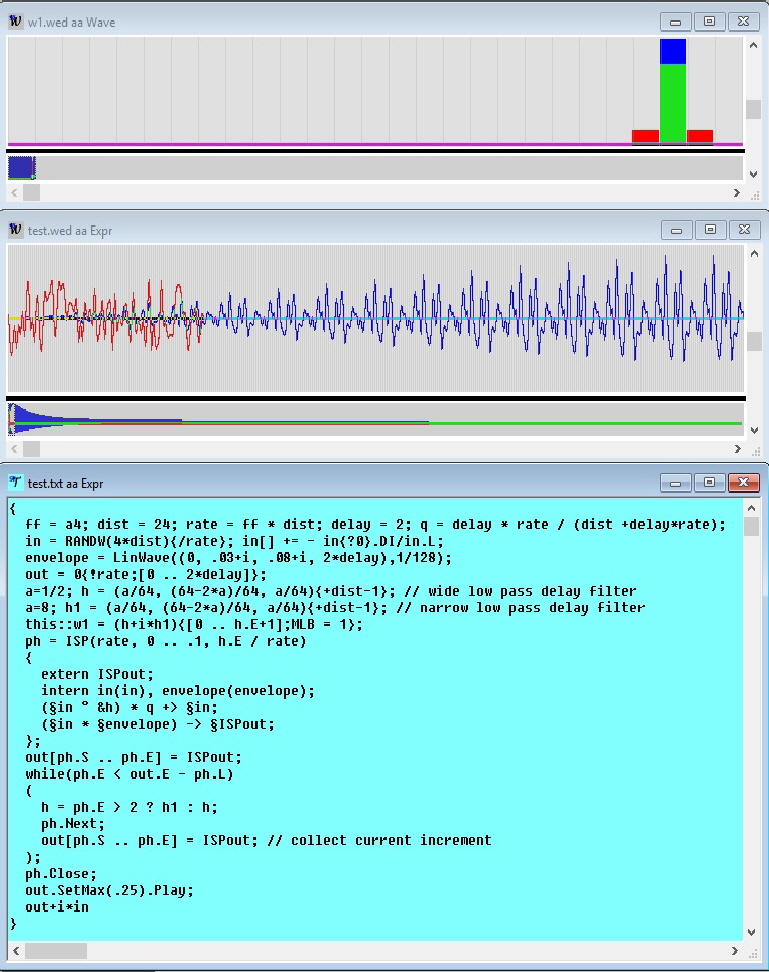
A permanent expression object with name “ThreeXHelloWorld” during execution is shown in the following screen-shot. This short application involves three tasks, the first is the main-task, started by pressing the button labeled “Run” on the Control-Bar; it consists of three three lines, each containing a command, and enclosed in braces. Playing the standard pitch for 2 seconds in Antonio can be done with the simple expression The following screen-shot shows a (slightly simplified) function htwist, which is frequently used in Antonio applications for the generation of an impulse; often the unit is considered as the prototype of an impulse, Unit(1) is 1 at time 0 and 0 for all other sample-points; it has a constant spectrum of amplitude 1 in the frequency range -1/2 .. 1/2; the htwist function tries to keep up to the same absolute spectrum, but spreads the impulse over several sample points; in addition, it allows to linearly reduce the intensity of high frequency dependent on the first parameter hp with values between 0 and 1; for hp == 1, the absolute spectrum of htwist is - within inaccuracies - identical to the spectrum of the unit-impulse. The second parameter hlen of htwist determines the degree of spreading, for hlen == 0 (and hp == 1), the resulting impulse is the unit-impulse; negative values of hlen let lower frequencies appear first, for positive values higher frequencies have precedence. The comb-filter repeats an impulse input at fixed intervals d again and again, the only change between repetitions is the repeated multiplication of the impulse with a damping-factor q; the corresponding (absolute) spectrum has equidistant resonances within the range -rate/2 .. rate/2, there is a resonance at frequency 0, then at + or - ff, + or - 2*ff, and so on, at all multiples of ff for -rate/2 < ff < rate/2, where ff = rate/d; in other words, for a comb filter all resonances are exact harmonics. A real resonator like a string in a piano has a similar resonance spectrum, however, there is no resonance for frequency 0 and the other components deviate from the exact harmonic spectrum, we say, a real string behaves like a comb-resonator with a slight skew; a slight skew is necessary in sound synthesis to achieve the kind of multiple beating between the components of a sound, that makes a sound attractive. The following screen-shot shows a function called CombAp, which behaves -. dependent on the parameters - as a more or less skewed resonator. CombAp combines a comb-resonator with distance d and factor q with an all-pass-resonator (or, if one prefers, phase-shifter) with distance ad and factor aq. The z-transform C(z) of the comb-resonator is (1-q)/(1-q*z^-d), the z-transform A(z) of the all-pass-resonator is (1-aq*z^ad)/(1-aq*z^-ad); we arrive at the z-transform CA(z) to CombAp by replacing the q in the denominator of C(z) with q*A(z), in other words, on repetitions CombAp not only applies a real factor q, but also a complex frequency-dependent factor with absolute value 1. The resulting z-transform CA(z) is shown on the first line in a rem statement, the incremental signal process in CombAp is an implementation of CA(z). It is easy to see, that CA(z) reduces to C(z) for aq == 0. In the following, q and and aq are derived from delays rather than given directly; the delay of a resonator can be understood as the weighted average length of its response, in case of an all-pass, it is understood as the weighted average length of the actually delayed and not immediately emitted response. Wave w1 shows in the real part (blue) the skewed output for a negative aq and in the imaginary part (red) the pure comb-output; evidently, the shape of repetitions of the pure comb remains the same (except for shrinking), while the skewed response changes the shape from repetition to repetition. Wave w2 shows the spectrum of the skewed response with negative aq in blue, of the skewed response with a positive aq in red, and without a skew in green; the green resonances are exactly equidistant.
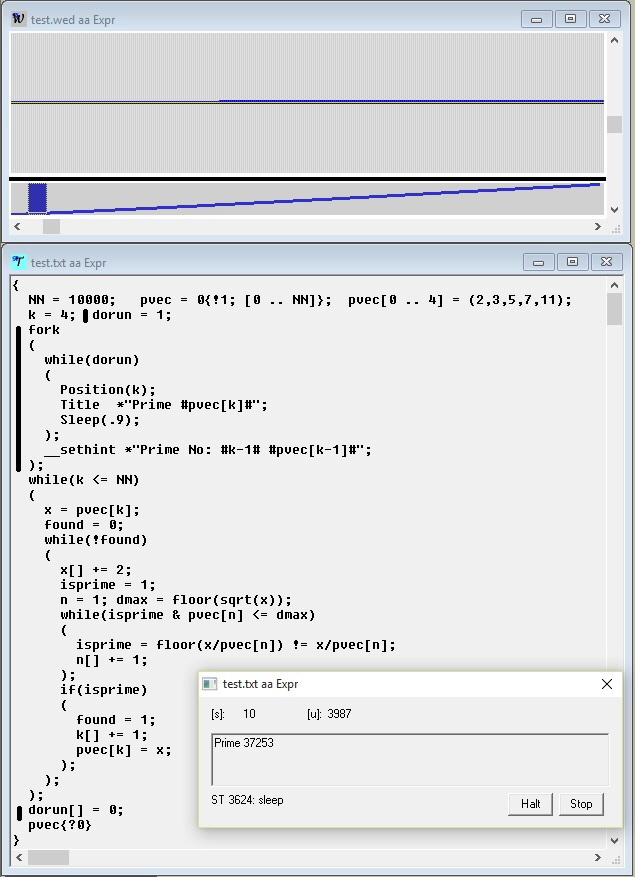
A complete program, which solves the following set of equations consider as example the simple fork command in line 4 of the test expr object: the handle is discarded, it is not needed; with the fork command, the subtask is started by the interpretation of the text between the fork keyword and the terminating semicolon. The original program collects the first NN prime numbers into a vector pvec. The code marked with a vertical bar has been added to monitor the progress of prime collection. Position(k) writes the current value of k into the [u] (user) field of the Expr-Dialog. Title string writes the string into the text field of the Expr-Dialog. One can see, that at the time, when the snapshot was taken, the 3987th prime with value 37253 had been collected; further, that the subtask has the thread number 3624 and was sleeping. The subtask runs in this case in the same environment as the invoking maintask. The variable dorun is used by the task to terminate the subtask; an alternative method to terminate a task and all its subtasks is, to click on the Stop-button of the Expr-Dialog
|
||||
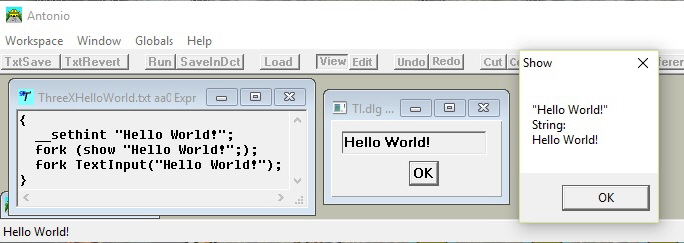 The effect of braces is, that the text object, while in execution, has its own dictionary. The first command places text on the status-bar; the second starts a subtask, which executes a
The effect of braces is, that the text object, while in execution, has its own dictionary. The first command places text on the status-bar; the second starts a subtask, which executes a